Decision Tree

决策树模型

下面引用下维基百科对决策树的描述:

机器学习中，决策树是 一个预测模型；他代表的是对象属性与对象值之间的一种映射关系。树中每个节点表示某个对象，而每个分叉路径则代表的某个可能的属性值，而每个叶结点则对应 从根节点到该叶节点所经历的路径所表示的对象的值。决策树仅有单一输出，若欲有复数输出，可以建立独立的决策树以处理不同输出。 数据挖掘中决策树是一种经常要用到的技术，可以用于分析数据，同样也可以用来作预测。

决策树分类原理

决策树是一个非常常用的机器学习算法，其中的一个重要的特点是简单，使用者基本上不用了解机器学习算法，也不用深 究它是如何工作的。直观看上去，决策树分类器就像判断模块和终止块组成的流程图，终止块表示分类结果（也就是树的叶 子）。判断模块表示对一个特征取值的判断（该特征有几个值，判断模块就有几个分支），非常简单直观。

使用决策树进行分类时，样本所有特征中有一些特征在分类时起到决定性作用，决策树的构造过程就是找到这些具有决定性作 用的特征，根据其决定性程度来构造一个倒立的树–决定性作用最大的那个特征作为根节点，然后递归找到各分支下子数据集 中次大的决定性特征，直至子数据集中所有数据都属于同一类。所以，构造决策树的过程本质上就是根据数据特征将数据集分 类的递归过程，我们需要解决的第一个问题就是，当前数据集上哪个特征在划分数据分类时起决定性作用。

ID3 算法

ID3 算法的核心思想就是以信息增益度量属性选择，选择分裂后信息增益最大的属性进行分裂。 如果\(\mathcal{D}\)为数据集，\(d^{(i)}\)表示第\(i\)个样本的类标，依此对训练数据进行的划分，则数据集\(\mathcal{D}\)中类标\(d\)的熵为：

\[H(d;\mathcal{D}) = -\sum_i^m{p(i)\log(p(i))}\]

其中\(p(i)\)表示第 i 个类别在整个训练数据中出现的概率，\(m\)表示\(d\)所有可能取值的个数，可以用属于此类别的数量除以训练数据总数量作为估计。 熵的实际上表示是混乱程度的一种度量， 当我们将训练集\(\mathcal{D}\)按属性 A 进行划分，则 A 对\(\mathcal{D}\)划分后的熵为:

\[H_A(d;\mathcal{D}) = \sum_{j\in A}{\frac{|\mathcal{D}_j|}{\mathcal{|D|}} H(d;\mathcal{D}_j)}\]

其中\(\mathcal{D}_j\)表示数据集\(\mathcal{D}\)中类标为\(d(j)\)的组成数据集，\(|\mathcal{D}_j|\)表示数据集\(\mathcal{D}_j\)的样本数 而信息增益则定义为上述两个熵的差值:

\[\text{gain}(A) = H(d;\mathcal{D}) - H_A(d;\mathcal{D})\]

ID3 算法就是在每次需要分裂时，计算每个属性的增益率，然后选择增益率最大的属性进行分裂。

C4.5 算法

ID3 算法存在一个问题，就是偏向于多值属性，例如，如果存在唯一标识属性 ID，则 ID3 会选择它作为分裂属性，这样虽然 使得划分充分纯净，但这种划分对分类可能是不利的。ID3 的后继算法 C4.5 使用增益率的信息增益扩充，试图克服这个缺点。 C4.5 算法用信息增益率来选择属性，克服了用信息增益选择属性时偏向选择取值多的属性，C4.5 定义的分裂信息可以表示成： \[\text{splitInfo}_A(d;\mathcal{D}) = \sum_{j \in A}{\frac{|\mathcal{D}_j|}{\mathcal{|D|}} \log(\frac{|\mathcal{D}_j|}{\mathcal{|D|}})}\] 然后，信息增益率被定义为： \[ \text{gainRatio(A)} = \frac{\text{gain(A)} } {\text{splitInfo}_A(d;\mathcal{D})}\] 在选择具有最佳分类效果的属性时，C4.5 算法是根据信息增益率来选择，而不是信息增益。

为了日后更好地理解决策树的构建，在维基百科上找了一张决策树的图，不过就不做具体分析了。

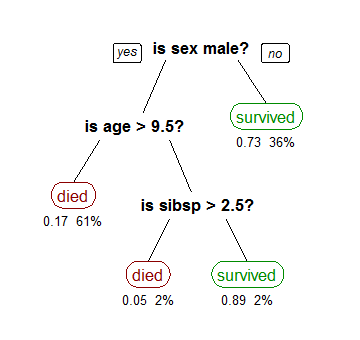
决策树优缺点

在网上搜索了关于决策树的优点和不足之处，现总结如下:

• 决策树适用于数值型和标称型（离散型数据，变量的结果只在有限目标集中取值），能够读取数据集合，提取一些列数据中蕴含的规则。
• 在分类问题中使用决策树模型有很多的优点，决策树计算复杂度不高、便于使用、而且高效，决策树可处理具有不相关特征的数据、可很容易地构造出易于理解的规则，而规则通常易于解释和理解。
• 决策树模型也有一些缺点，比如处理缺失数据时的困难、过度拟合以及忽略数据集中属性之间的相关性等。